Nathaniel B,
   Let me say that your post has a lot of math that I am too sick to follow completely to identify the specific problem.  Instead, I would like to go back to some first principles of the algorithm and see if I can summarize what you say your math proves.

   
     
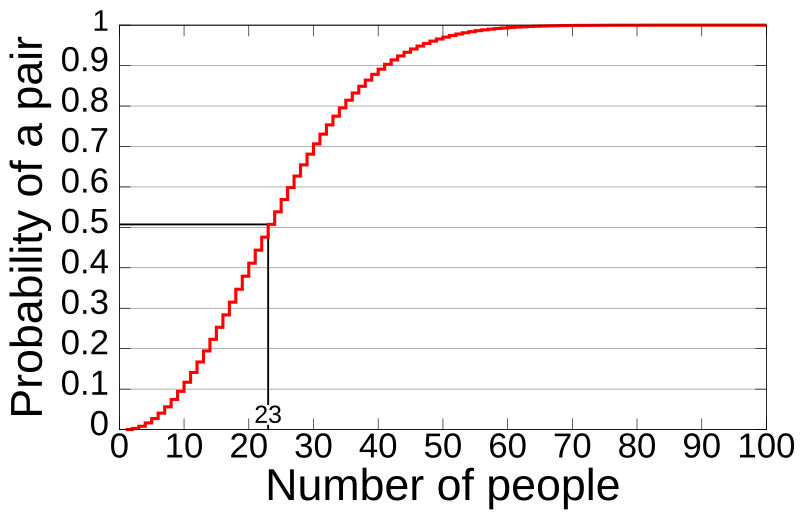
   Based upon this graph it would appear that it all depends upon how far up the curve you set your target.    If you set the target below 23 then you have non linear increases in probability of finding someone.  If you set it above 23 it scales approximately linearly until you hit 40 at which point you start getting less and less benefit by increasing your RAM. 

   Now, with this hash algorithm the total hash power is proportional to the AREA under the curve.   The first person you add has 0 chance.  Everyone less than 10 has less than 10% chance.  Every hash over 23 has a 50% chance.    So performance is clearly tied to how quickly you can increase your probability of finding a result which of course has diminishing returns. 

   Clearly, once you get near 50 people your memory usage can become constant and you will have 95% of the hash power that you would have if your doubled your memory.   Fortunately, we limit the NONCE search space which prevents you from ever going past ~23.    So I stay on the portion of the curve that does gain by increasing RAM.   

 
 
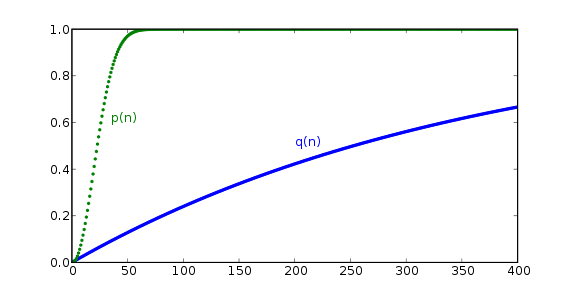
   Taken to the extreme, of only having memory for 1 birthday you would end up on Q(n) curve. 

   There are two approaches to finding a collision and you can make a trade off of memory for parallelism.    So let me try some math here...

   Lets assume you only have memory for 10 items (50% of target) then your probability of finding a result is .1 * P  where P is the level of parallelism.  As a result if P is 10 then the probability of finding a result after 1 step is 50/50.

   Lets assume P is 1 in the CPU case.   Now instead of doing 10 calculating in parallel you do them sequentially.   In this case after you have performed 10 steps your next calculation is 50/50 which is equal to the parallel case, except that you get the benefit of the area under the curve which means that on average it will take you less than 10 steps to find the result.  Also, in the GPU case the cost of trying again is another 10 checks in parallel, where as the cost of the CPU case with memory increase is less than 1 additional calculation.   

   Conclusion:  reducing memory does cause a linear reduction in the probability of finding one collision,  but you must take the area under the curve to see the true benefits.

   Now at this point you may point out that the GPU could do the first 10 steps in parallel and thus the GPU could have a 50/50 chance of having solved it in 2 steps while the CPU would be 10 steps behind.    I do not think this would be the case however with a 50 bit birthday space. 

Anyway, the proof is in the implementation.   
   
 

Quote from: petregr on November 06, 2013, 08:08:23 pm

Quote from: bahamapascal on November 06, 2013, 08:05:19 pm

LOL, first it was 0.09 (which was oviusly a mistake) then he changed it to 0.009...and now its 0.0009 

Mistake, hah...just watch how many people said that price is not correct!

So how changed the 0.009 to 0.0009? The owner of this thred or the admin?

I changed it.

Lets just say that we were not able to mine as much as we wanted to and are trying to make up lost ground by buying on the market.

Cannot let Lighthouse run away with it all

Quote from: wickedcoin on November 06, 2013, 04:31:07 pm

Oops. Yeah that was supposed to be 1,000 not 10,000. Sorry. I'm looking to by more but Super3 will handle that for me.

can you clarify: 0.09 or 0.009 PTS/BTC?

Are you still wanting to buy at .009?

Quote from: bytemaster on November 06, 2013, 06:56:40 pm

Quote from: atavacron on November 06, 2013, 06:44:12 pm

Quote from: bytemaster on November 06, 2013, 06:39:35 pm

Post in this thread if you are interested.

I'll do 2,000 PTS @ 0.0026 BTC / PTS

Ok... so 5.2 BTC for 2000 PTS!

PTS Address: PbQRDzvkUxm7Qrf5yVGAaCVcR5nYqSdN9S

PTS sent...

TxID:  f238323ea3ef45582d2854b99635ff1c510df3e7b8cc490bee6a2c29a5f593bb


My BTC Address:  1JjRvKbtin5X5vSi3XJEWdHc8YbNJhALzz

Received, but I am going to wait until 12 confirmations due to the current potential for orphans..

Quote from: bytemaster on November 06, 2013, 06:39:35 pm

Post in this thread if you are interested.

I'll do 2,000 PTS @ 0.0026 BTC / PTS

Ok... so 5.2 BTC for 2000 PTS!

PTS Address: PbQRDzvkUxm7Qrf5yVGAaCVcR5nYqSdN9S